МЕТОДЫ ПОВЫШЕНИЯ ТОЧНОСТИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

14.1. Системный подход к планированию объемов испытаний подсистем

Традиционно при проведении испытаний подсистем требования к ним определяются путем декомпозиции требований к системе в целом. При большом числе подсистем такие автономные требования настолько ужесточаются, что подтверждение их по проводимому на практике объему испытаний становится нереальным. Так, если требуемая ве­роятность безотказной работы изделия составляет 0,9, то при числе подсистем к = 10 их надежность должна быть 0,99, а при к — 100 — 0,999. Для подтверждения одной девятки с доверительной вероятно­стью 0,9 достаточно испытать изделие 23 раза, для двух девяток — 230 раз, а для трех девяток — 2303 раза.

Системный подход к планированию объема испытаний подсис­тем позволяет избежать лавинообразного нарастания требуемых объе­мов испытаний. Он заключается в построении оценок и доверитель­ных интервалов показателей эффективности системы по известным оценкам показателей эффективности подсистем и обосновании тре­бований к объему их испытаний, исходящих из анализа свойств оце­нок системы в целом.

Подтверждение требований к вероятности выполнения задачи.

Пусть вероятность выполнения задачи R связана с аналогичными ве­роятностями для подсистем Rj мультипликативной зависимостью:

к

R=Y1R,.

/=1 1

Далее пусть в результате проведения автономных испытаний получе­ны данные по каждой подсистеме {/и(, л(}, і = 1,…, к. Необходимо определить оценку вероятности R и ее точность. Оценка вероятности выполнения задачи для каждой подсистемы определяется по частоте успешных исходов:

Ri=milni.

Оценка вероятности выполнения задачи системой в целом опре­деляется в соответствии с принятой моделью:

. к Л

R= П Rg.

/=1

Точность этой оценки характеризуется у%-ным доверительным ин­тервалом [7^, /у, где *„ = ЭКВ’ тэкв> v)> Лв ^В^ЭКВ’ ^ЭКВ’ при лэкв = тіп{л,}, /Иэи =/{/1э КВ /— целая часть [88].

Интересен частный случай, практически важный для высокона­дежных систем, когда при автономных испытаниях не наблюдалось отказов ни по одному виду подсистем (ntj = л(). Тогда для изделия в целом выполняется тэкв = пэкв и нижняя доверительная граница рассчитывается из соотношения

= 1-у.

В этом случае легко обосновать объем испытаний, необходимый для подтверждения требований как к системе в целом, так и к отдельной ее подсистеме:

‘Ъкв =ni =In(1-Y)/ln^J-

Проанализируем принципиальное отличие предложенного под­хода от сложившейся практики задания требований к каждой подси­стеме путем дробления общих требований к системе.

Пусть заданная вероятность выполнения системой поставленной перед ней задачи составляет Л, = 0,9, а доверительная вероятность, с которой необходимо подтверждение данного требования, у = 0,9. Си­стема состоит из 10 последовательно соединенных подсистем. Тради­ционный путь заключается в нахождении требований = 0» 99

и определении объема испытаний

= In (1 — y)/ln = 230.

При применении предложенного системного подхода необходи­мый объем автономных испытаний рассчитывается исходя из требо­ваний к системе в целом и составляет «,• = In (1 — y)/ln = 23.

Подтверждение требований к среднему значению. Пусть показа­тель эффективности системы представляет собой сумму показателей эффективности подсистем:

М = Y*mj-

j=і

Измерение показателей эффективности происходит в соответствии с моделью Xjj = ntj +5у, где bjj ~ N(О, Оу j — нормально распреде­ленная случайная погрешность измерения с нулевым математичес­ким ожиданием и известной дисперсией с?-. Оценкой показателя эф­фективности ntj является среднеарифметическая оценка

— 1 ?

7 /=1

при этом у%-ный доверительный интервал определяется по формуле

*7 — “(1п)/2>ЯА/ — mi — *7 + “(1+т)/2>ЯА/ •

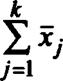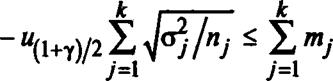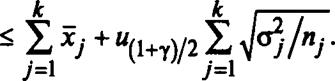Суммируя доверительные интервалы для подсистем, получим оценку показателя эффективности системы, рассчитанную по резуль­татам автономных испытаний:

Перейдем к усиленным неравенствам "(*7 + г *• "(*/ -“(Щ)/2

пип ‘ ‘ Jl ■’/щах

выполнение которых обеспечивает выполнение исходного равенства.

Из усиленных неравенств немедленно следуют требования к ма­тематическим ожиданиям подсистем при автономном подходе:

где = M3/n.

При системном подходе строится закон распределения оценки к

х = £ Xj, представляющий собой нормальное распределение с мате­рі к

матическим ожиданием М = £ ntj и дисперсией

7=1

В соответствии с нормальным законом распределения у%-ный доверительный интервал при системном подходе запишется в виде

к _ Гк — к _ Гк —

X Х) ~И(1п)/2 JX ®у/Яу * М * X *7 +и(Щ)/2 JX ®у/Яу — 7=1 )(7=1 7=1 17=1

Требования к показателям эффективности подсистем определя­ются в этом случае как

{*} — “0- (*У + "(і+ї)/2>Щ^)тіп •

Таким образом, дисперсия оценки хопределяющая ширину доверительного интервала и соответственно погрешность принимае­мого статистического решения, при системном подходе в — Ik раз мень­ше, чем при автономном.

Подтверждение требований к дисперсии. В рассматриваемой в предыдущем разделе аддитивной модели принимались известными

у

дисперсии Оj (/= 1,…, п). При неизвестных дисперсиях требование к математическому ожиданию может быть дополнено требованием к

дисперсии. Таким образом, имеем о2 = £ Оу.

У=1

Оценкой дисперсии <Ту, полученной по результатам автономных испытаний, является оценка вида

при этом статистика Sj (rij — l)/<jy имеетх2-распределение с (л,- -1)

степенями свободы, а соответствующий доверительный интервал находится в пределах

Х(|п)/2 ("> 0 " Х(1_т)/2 (”У — »)

В качестве оценки дисперсии системы естественно принять ве­личину

■s2 = і s).

У=і

Эта оценка в соответствии с правилом Сэттервейта [27] может быть аппроксимирована ^-распределением с числом степеней сво­боды v, рассчитываемым по формуле

В зависимости от конкретных значений оценок Sj величина v меняется в диапазоне

к

min {rij} < v < X («у -!)

у=1

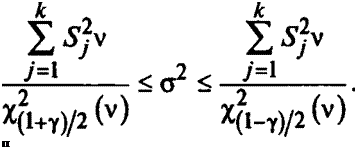и достигает своего наибольшего значения при равных S.-, rtj. При этом у%-ный доверительный интервал для дисперсии системы имеет вид:

Последовательно заменяя ^ Sj на Sj

7=1

бования к дисперсиям отдельных подсистем:

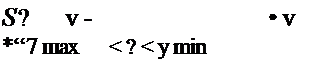Х(і+ї)/2 (v) 3 X(,_Y)/2 (v)

Так как v, как правило, оказывается больше, чем (и. — 1), сис­темный подход обеспечивает определенное сужение доверительного интервала. Конкретная величина выигрыша от использования сис­темного подхода рассчитывается после получения эксперименталь­ных данных (табл. 14.1).